Notorious primary school exam questions
As kids, we may have believed that adults were much wiser than us. Now that we’re all grown up, it’s time to put that theory to the test and see if we’re indeed much smarter than we were back then…by testing ourselves with some primary school exam questions.
Without triggering any childhood trauma, here are nine of the most notorious exam questions from the bygone years of our primary school days that will put even Helen and Ivan to shame:
English
1. 2012 – Special expressions

Image credit: P6 English SA1 2012 – Nan Hua
Answer:
(3) cleared
Explanation:
Don’t be ashamed if you chose “clear” as the answer initially, as you might think that the present tense is correct here since Tina technically hasn’t cleaned her room yet. However, when we use the expression “it’s time”, the verb form that follows the subject must be in the past tense.
Here’s a clearer explanation from Cambridge Dictionary:

Image adapted from: Cambridge Dictionary
2. 2013 – Auxiliary verbs

Image credit: P6 English Prelims 2013 – CHIJ
Answer:
(3) each
Explanation:
While this question may not be the most difficult, those who jumped the gun and immediately assumed the answer was “both” after seeing “two stories” would’ve been wrong. The correct answer should be “each”, since the auxiliary verb “was” is singular.
Science
3. 2018 – Expansion and contraction
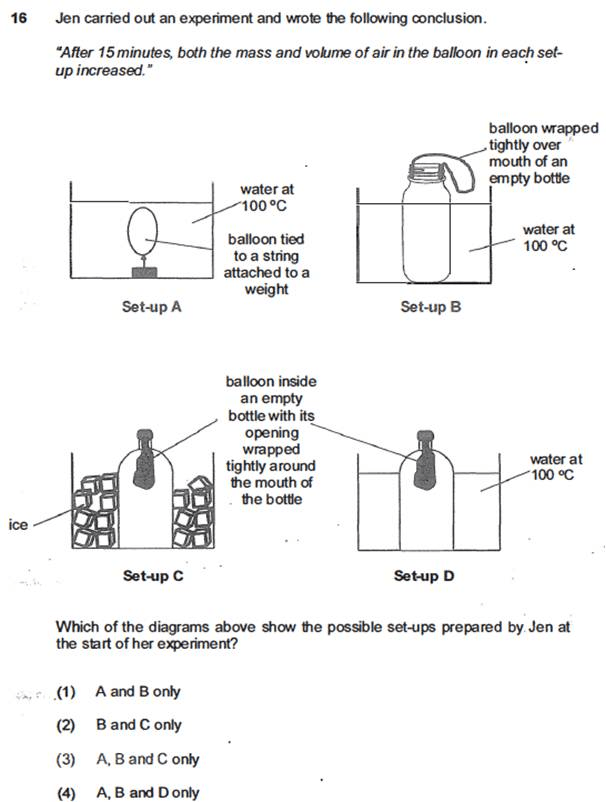
Image credit: Kiasu Parents
Answer:
(2) B and C only
Explanation:
Many would have no problem identifying that set-up B is the most plausible set-up, since it’s literally in each of the multiple choice answers.
Next, we gotta remember that air expands when heated and contracts when cooled. Since the bottle in set-up C is surrounded by ice, the air in the bottle will contract, creating space in the bottle. This pressure difference between the air outside and inside would cause air from outside to enter the balloon, thus increasing the balloon’s mass and volume.
4. 2009 – Centre of gravity
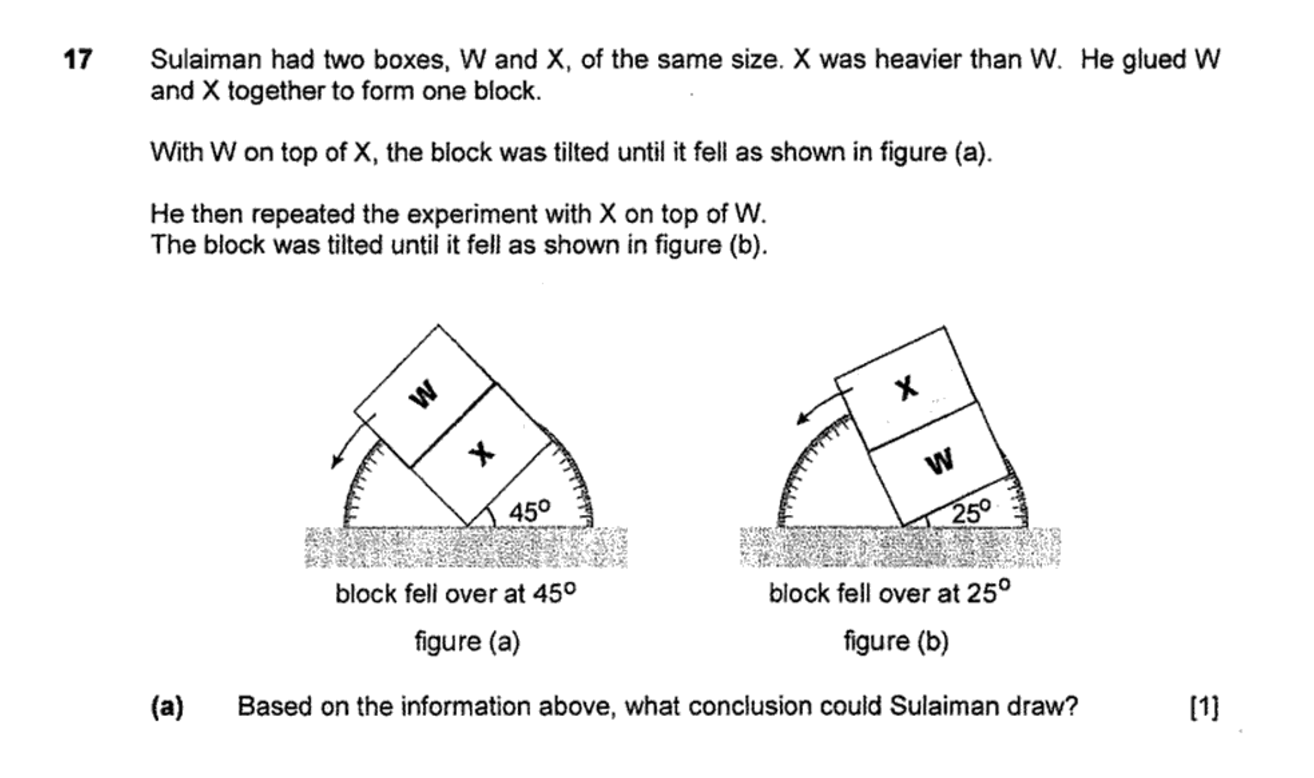
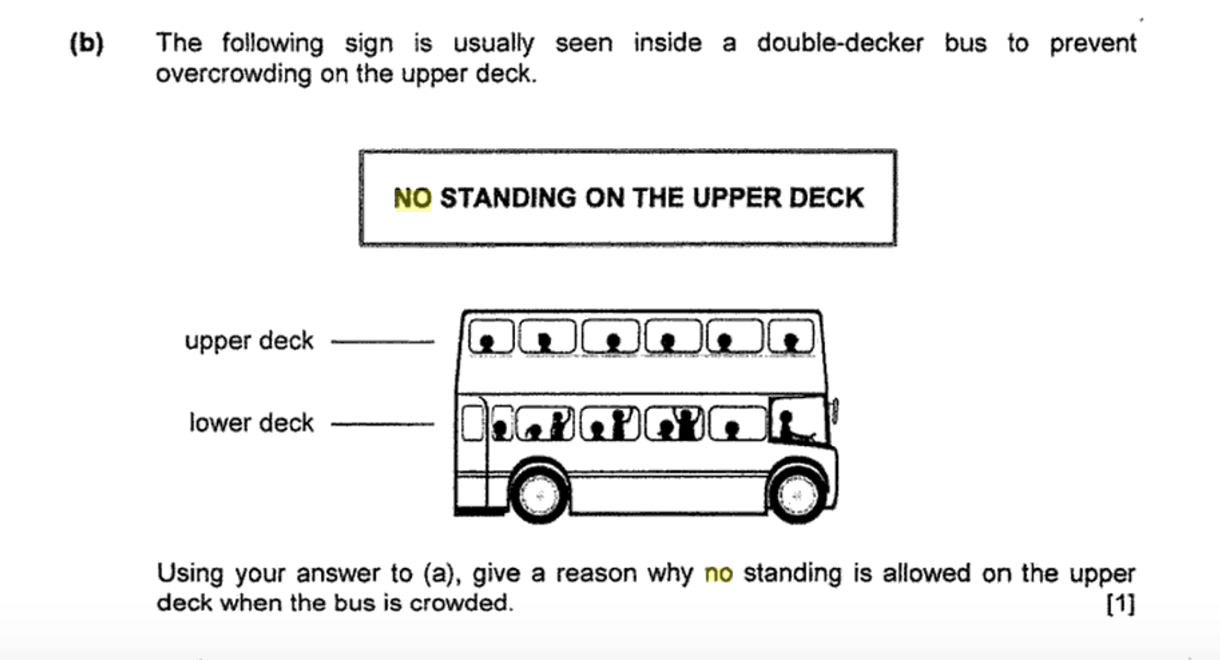
Image credit: PSLE Examination Questions, pg 91, Hillview
Answer:
a) The higher the centre of gravity/mass, the lower the tilt angle required to topple.
b) When a person stands on the upper deck of a double-decker bus, their centre of gravity is higher, and thus increases the risk of the double-decker falling when turning.
Explanation:
The first portion comes from textbook knowledge, and shouldn’t be too difficult to infer from the question. Essentially, when an object is top-heavy, it will have a higher centre of gravity. This means that less tilt is needed to topple the entire block, as it’s easier to destabilise the higher centre of gravity object compared to an object with a lower centre of gravity.
The second portion, however, requires real-world knowledge and application, which is where many students may falter. A low centre of gravity is essential for stability, but having standing passengers on the upper deck increases the centre of gravity and destabilises the bus. This would cause the bus to be more prone to toppling.
5. 2019 – Magnetic induction
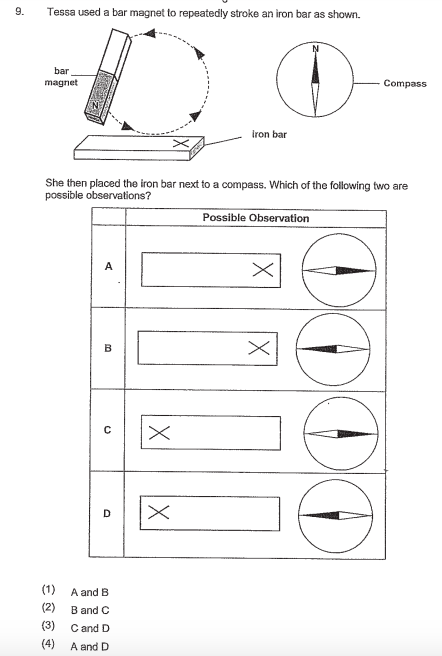
Image credit: P6 Science 2019 SA1 ACS Junior
Answer:
(2) B and C
Explanation:
When you stroke an iron bar anti-clockwise with the north pole of a magnet, the iron bar will be magnetised with the “north” side on the left and the “south” side on the right. This is because the north pole of the magnet will always induce a north pole at the first point of contact.
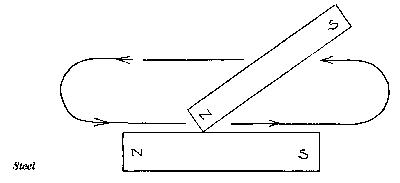
Image credit: The Free Dictionary
Therefore, we know the “X” is the south pole, which will attract the black part of the needle which is “north”. The same goes for the north pole of the iron bar, which attracts the “south” side of the compass needle.
Maths
6. 2021 – Geometry
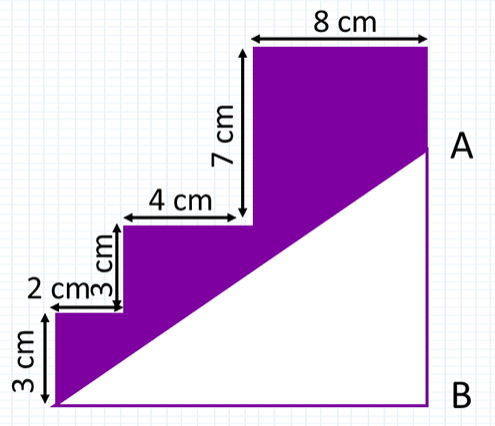
Image credit: Practicle
The perimeter of the shaded part is 4CM more than that of the unshaded part. What is the length of AB?
Answer: 11CM
Explanation:
This question comes from the same paper as the infamous Helen and Ivan question, and is just as challenging in its own right.
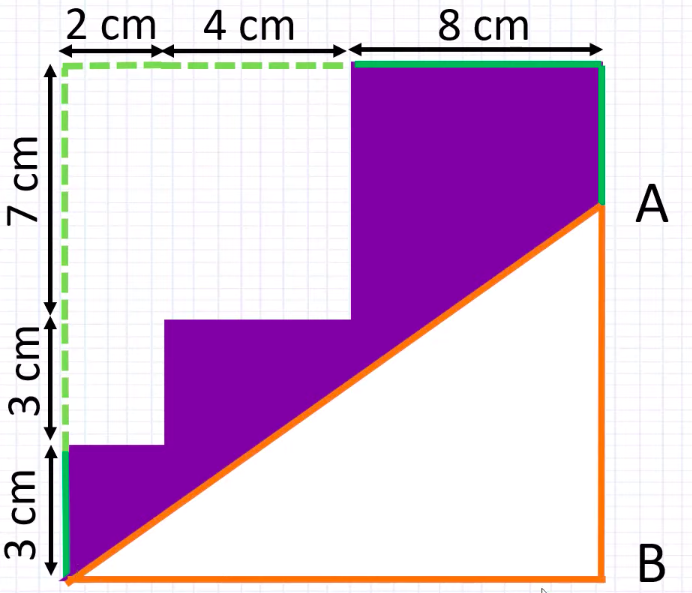
Image adapted from: Practicle Math
If you’re able to extrapolate the perimeter of the shaded area into a rectangular figure, you’ll notice that the diagonal corner and the length of the rectangle (8CM + 4CM + 2CM) of the shaded and unshaded figure cancel each other out.
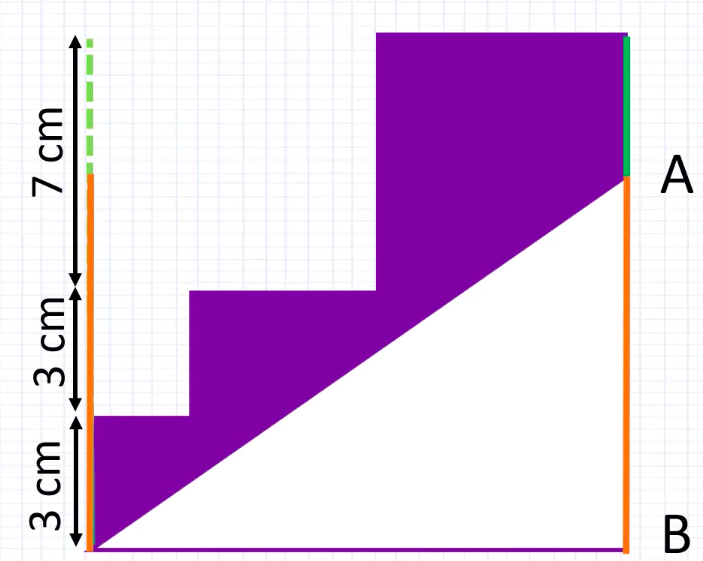
Image adapted from: Practicle Math
This leaves us with the green lines in the image above, which makes up the 4CM difference between the shaded and unshaded part. Divide it by 2 and we will solve for the length of one of the green lines.
Therefore, the length of AB = 3 + 3 + 7 – 2 = 11CM
7. 2016 – Fractions
Suyin baked some pies. She gave 1/5 of them to her relatives and 30 of them to her friends. She was left with 2/3 of the pies. Then she packed these into 18 boxes. Some boxes contained 6 pies while the rest contained 12.
a) How many pies were packed into the 18 boxes?
b) How many boxes contained 6 pies?
Answer:
a) 150 pies
b) 11 boxes
Explanation:
a) Everyone loves pie, but not when it’s in our maths questions. The first portion should be quite straightforward, as it just involves converting the fractions into their common denominator and realising that 30 = 2/15 of the pies. This means the total pies Suyin baked at the start is 225.
2/3 x 225 = 150
b) The second part is where it gets tricky. Since there are 18 boxes in total, let’s assume that each box has 6 pies instead.
6 x 18 = 108 pies, but since we have 150 pies in total and not 108, there are 42 pies that could’ve been packed into boxes of 12.
Since each box requires just 6 more pies to make a box of 12, 42 ÷ 6 = 7, meaning there are 7 boxes that could hold 12 pies each. Take 18 – 7 = 11 and we’ll have the answer.
8. 2020 – Fractions part 2
John had 1/3 as many erasers as pens. He went to a class and gave each student 4 erasers and 3 pens. Subsequently, he discovered that he had 6 erasers and 180 pens left.
a) How many students were there in the class?
b) How many erasers did John have at first?
Answer:
a) 18
b) 78
Explanation:
This question requires you to draw out a bar model in order to visualise the solution.
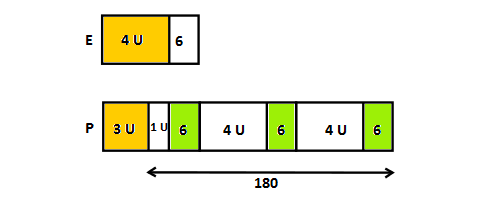
Image adapted from: Singapore Math Guru
a) Since 9 units + 18 = 180, each unit equals to 18. The number of pens given out is 3 x 18 = 54. As each student was given 3 pens each, the number of students there = 54 ÷ 3 = 18.
b) With the number of each unit identified, solving for part (b) should be a cakewalk. The number of erasers John has at the start is 18 x 4 + 6 = 78.
9. 2000 – Number sequences

Image credit: Singapore PSLE Mathematics Extreme Drill Questions
Answer:
(C) 3
Explanation:
We’re only concerned with the digit in the ones place of the final number, so all we have to do is add up the digits in the ones place from 1 + 2 + 3 + 4 + 5….+ 94 + 95 + 96 + 97.
(1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 0) x 9 + (1 + 2 + 3 + 4 + 5 + 6 + 7) = 433
Since 3 is the digit in the ones place when we add up all the ones digits, it will also be the digit in the ones place for the final number. Therefore, the answer is 3.
Difficult primary school exam questions in Singapore
If you clicked on this article thinking that it would be a breeze going through these questions meant for 12-year-olds only to end up pulling out half your hair, that’s exactly what we went through as well.
Between homework, supplementary classes, tuition, and exams, being a child is not entirely stress-free in Singapore. And yes, although having a magical pill that allows us to experience our youth again would be nice, thinking about going through school one more time just makes it that much harder to swallow.
For the sadistic, check out more exam-related articles:
Cover image adapted from: Singapore Math Guru
Illustrated by Charlotte Lee.





